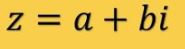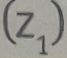Para representar los
números complejos, debemos salir de la recta numérica y recurrir al
plano cartesiano.
El número
complejo
se representa en el plano mediante el punto de coordenadas
El eje de las abscisas (x) se llama eje real, y el de las ordenadas (y), eje imaginario. De esta forma a cada número complejo le corresponde un punto del plano cartesiano y a cada punto del plano le corresponde un numero complejo.
Se representa en el plano mediante el punto de coordenadas